概率论与数理统计#

1.随机事件与概率#

1.1 基础概念#

随机试验：试验是指为了察看某事的结果或某物的性能而从事的某种活动. 在概率论与数理统计中，一个试验如果具有以下3个特点:

(1) 可重复性: 在相同条件下可以重复进行：
(2) 可观察性: 每次试验的可能结果不止一个，并且能事先明确试验的所有可能结果:
(3) 不确定性: 一次试验之前，不能预知会出现哪一个结果。就称这样的试验是一个随机试验，也简称为试验。

样本点和样本空间：
每次试验的每一个结果称为基本事件，也称作样本点，记作 $w_{1}, w_{2}, \cdots$ 全部样本点的集合称为样本空间，记作 $\Omega,$ 则 $\Omega=$ $\left\{w_{1}, w_{2}, \cdots\right\}$
例子:
投郑一颗均匀股子，观察出现的点数。这是一个随机试验。样本空间 $\Omega=\{1,2,3,4,5,6\} .$
随机事件：
基本事件是不可再分解的、最基本的事件，其他事件均可由它们复合而成，由基本事件复合而成的事件称为随机事件或简称事件。常用大写字母 $A, B, \quad C$ 等表示事件。比如 $A=\{$ 出现的点数为偶数 $\}=\{2,4,6\} .$

1.2 随机事件与概率#

随机事件在一次试验中是否发生虽然不能确定，但让人感兴趣的是随机事件在一次试验中发生的可能性有多大。概率就是用来描述随机事件发生的可能性大小的。比如抛硬币的试验，拖得次数越多，出现正面的次数与投郑次数之间的比例（也叫频率 )愈加趋于0.5。它的数学定义为: = :
在多次重复试验中，若事件A发生的频率稳定在确定常数 $p$ 附近摆动，且随着试验次数的增加，这种摆动的幅度是很微小的。则称确定常数p为事件A发生的概率，记作 $P(A)=p .$
思考题
设一年有365天，求下列事件 $A, B$ 的概率:
$A=\{$n个人中没有2人同一天生日 $\}$
$B=\{$ n个人中有2人同一天生日 $\}$
解
显然事件 $A, \quad B$ 是对立事件, $P(B)=1-P(A)$. 由于每个人的生日可以是365天的任意一天，因此， $n$ 个人的生日有 $365^{n}$ 种可能结果，而且每种结果是等可能的，因而是古典概型，事件A的发生必须是 $n$ 个不同的生日，因而 $A$ 的样本点数为从365中取 $n$ 个的排列数 $P_{365}^{n},$ 于是
$$ \begin{array}{c} P(A)=\frac{P_{365}^{n}}{365^{n}} \\ P(B)=1-P(A)=1-\frac{P_{365}^{n}}{365^{n}} \end{array} $$

1.3 条件概率#

定义设 $A, B$ 是两个事件，且 $P(A)>0,$ 则称
$$ P(B \mid A)=\frac{P(A B)}{P(A)} $$ 为在事件A发生的条件下，事件B的条件概率。例子某种元件用满6000h未坏的概率是3/4，用满10000h未坏的概率是1 $/ 2$ ，现有一个此种元件，已经用过 $6000 h$ 未坏，试求它能用到10000h的概率。解设A表示\{用满10000h未坏\}, $B$ 表示\{用满 $6000 h$ 未坏\}, 则 $$ P(B)=3 / 4, P(A)=1 / 2 $$ 由于 $A \subset B, A B=A,$ 因而 $P(A B)=1 / 2,$ 故 $$ P(A \mid B)=\frac{P(A B)}{P(B)}=\frac{P(A)}{P(B)}=\frac{\frac{1}{2}}{\frac{3}{4}}=\frac{2}{3} $$

1.4 事件的独立性#

定义如果事件B发生的可能性不受事件A发生与否的影响，即 $$ P(B \mid A)=P(B) $$ 则称事件B对于事件A独立.显然，若B对于A独立，则 $A$ 对于 $B$ 也一定独立，称事件 $A$ 与事件 $B$ 相互独立. 例子. 口袋里装有5个黑球与3个白球，从中有放回地取2次，每次取一个，设事件A表示第一次取到黑球，事件B表示第二次取到黑球，则有 $$ P(A)=\frac{5}{8}, P(B)=\frac{5}{8}, P(A B)=\frac{5}{8} \times \frac{5}{8}=\frac{25}{64} $$ 因而 $$ P(B \mid A)=\frac{P(A B)}{P(A)}=\frac{5}{8} $$ 因此， $P(B \mid A)=P(B),$ 事实上还可以算出 $P(B \mid \bar{A})=P(B)$ 。这表明不论 $A$ 发是不发生，都对 $B$ 发生的概率没有影响。即B 与A独立.

性质：
事件 $A$ 和事件 $B$ 相互独立的充分必要条件是
$$ P(A B)=P(A) P(B) $$

2.全概率公式和贝叶斯公式#

2.1 全概率公式#

定义：
如果事件 $A_{1}, A_{2}, \cdots, A_{n}$ 是一个完备事件组，并且都具有正概率，则有：
$$ \begin{array}{c} P(B)=P\left(A_{1}\right) P\left(B \mid A_{1}\right)+P\left(A_{2}\right) P\left(B \mid A_{2}\right)+\cdots+P\left(A_{n}\right) P\left(B \mid A_{n}\right) \\ =\sum_{i=1}^{n} P\left(A_{i}\right) P\left(B \mid A_{i}\right) \end{array} $$ 对于任何事件 $B,$ 事件 $A \bar{A}$ 构成最简单的完备事件组，根据全概率公式得 $$ \begin{aligned} P(B) &=P(A B+\bar{A} B)=P(A B)+P(\bar{A} B) \\ &=P(A) P(B \mid A)+P(\bar{A}) P(B \mid \bar{A}) \end{aligned} $$

2.2 贝叶斯公式#

定义：
设 $A_{1}, A_{2}, \cdots, A_{n}$ 是一完备事件组，则对任一事件 $B, P(B)>0,$ 有
$$ P\left(A_{i} \mid B\right)=\frac{P\left(A_{i} B\right)}{P(B)}=\frac{P\left(A_{i}\right) P\left(B \mid A_{i}\right)}{\sum_{i=1}^{n} P\left(A_{i}\right) P\left(B \mid A_{i}\right)} $$
以上公式就叫贝叶斯公式，可由条件概率的定义及全概率公式证得。

例子:
市场上供应的某种商品只由甲、乙、丙3个厂生产，甲厂占45%，乙厂占35%，丙厂占20%。如果各厂的次品率依次为 4%, 2%, 5% 。现从市场上购买1件这种商品，发现是次品，试判断它是由甲厂生产的概率。
设事件 $A_{1}, A_{2}, A_{3},$ 分别表示“商品为甲、乙、丙厂生产的”，事件 $B$ 表示“商品为次品”，由题意得到概率
$$ \begin{array}{c} P\left(A_{1}\right)=45 \%, P\left(A_{2}\right)=35 \%, P\left(A_{3}\right)=20 \% \\ P\left(B \mid A_{1}\right)=4 \%, P\left(B \mid A_{2}\right)=2 \%, P\left(B \mid A_{3}\right)=5 \% \end{array} $$ 根据贝叶斯公式，可得: $$ \begin{aligned} P\left(A_{1} \mid B\right) &=\frac{P\left(A_{1}\right) P\left(B \mid A_{1}\right)}{P\left(A_{1}\right) P\left(B \mid A_{1}\right)+P\left(A_{2}\right) P\left(B \mid A_{2}\right)+P\left(A_{3}\right) P\left(B \mid A_{3}\right)} \\ &=\frac{45 \% \times 4 \%}{45 \% \times 4 \%+35 \% \times 2 \%+20 \% \times 5 \%} \approx 0.514 \end{aligned} $$ 在“购买一件商品”这个试验中， $P\left(A_{i}\right)$ 是在试验以前就已经知道的概率，所以习惯地称为先验概率。试验结果出现了次品（即 $B$ 发生），这时条件概率 $P\left(A_{i} \mid B\right)$ 反映了在试验以后对 $B$ 发生的“来源”(即次品的来源）的各种可能性的大小，通常称为后验概率。

3.随机变量#

3.1 随机变量#

把试验的结果与实数对应起来，随试验结果的不同而变化的量就是随机变量，包含离散型随机变量和连续型随机变量。例子：
郑一枚匀称的硬币，观察正面、背面的出现情况。这一试验的样本空间为 $\Omega=\{H, T\}$, 其中，H表示”正面朝上”, $T$ 表示“背面朝上”。如果引入变量 $X$ ，对试验的两个结果进行数值化，将 $X$ 的值分别规定为1和0，即 $$ X=\left\{\begin{array}{ll} 1 & \text { if } \text { 出现 } H \\ 0 & \text { if } & \text { 出现 } T \end{array}\right. $$ 这里的 $X$ 就叫随机变量，因为它能取的值是离散的，我们就叫它离散型随机变量。

3.2 概率分布#

定义：设离散型随机变量 $X$ 的所有可能取值为 $x_{1}, x_{2}, \cdots, x_{n},$ 称为 $X$ 的概率分布。
离散型随机变量 $X$ 的分布律具有下列基本性质：

$p_{k} \geq 0, k=1,2, \cdots$
$\sum_{i=1}^{+\infty} p_{k}=1$
二项分布：
二项分布是一种离散型的概率分布。二项代表它有两种可能的结果：成功或者不成功。每次试验必须相互独立，重复n次，并且每次试验成功的概率是相同的，为 $p $; 失败的概率也相同，为 $1-p$。掷硬币就是一个典型的二项分布。当我们要计算抛硬币吻，恰巧有 $x$ 次正面朝上的概率，可以使用二项分布的公式:
$$ P\{X=k\}=C_{n}^{k} p^{k}(1-p)^{n-k} $$

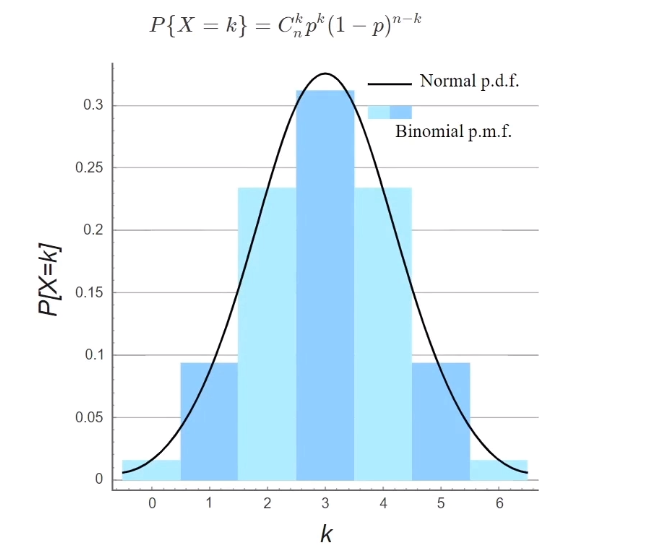
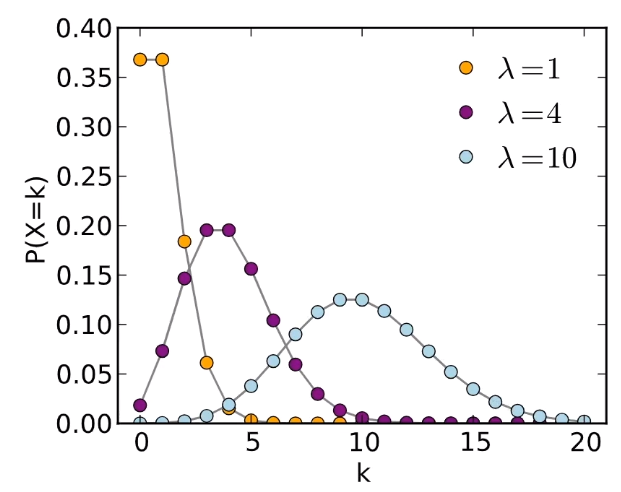
jupyter

泊松分布：
如果随机变量 $X$ 的概率分布为 $$ P\{X=k\}=\frac{\lambda^{k}}{k !} e^{-\lambda}, k=0,1,2, \cdots $$ 式中， $\lambda>0$ 为常数，则称随机变量 $X$ 服从参数为 $\lambda$ 的泊松(Possion)分布，记为 $X \sim P(\lambda)$.

jupyter

3.3 概率密度函数#

定义：若存在非负函数 $f(x)$, 使一个连续型随机变量 $X$ 取值于任一区间 $(a, b]$ 的概率可以表示为 $$ P\{a<X \leq b\}=\int_{a}^{b} f(x) d_{x} $$

正态分布：
正态分布是概率论中最重要的连续型分布，在19世纪前叶由德国数学家高斯（Gauss）加以推广，故又常称为高斯分布。正态分布的概率密度函数曲线呈钟形，概率密度函数为 $$ f(x)=\frac{1}{\sqrt{2 \pi} \sigma} e^{-\frac{(x-\mu)^{2}}{2 \sigma^{2}}} $$ 具有两个参数 $\mu$ 和 $\sigma^{2}$ 。第一参数 $\mu$ 是代表服从正态分布的随机变量的均值，第二个参数 $\sigma^{2}$ 是此随机变量的方差。如果一个随机变量服从均值为 $\mu,$ 标准差为 $\sigma$ 的正态分布，数学上记作 $$ X \sim N\left(\mu, \sigma^{2}\right) $$ 我们通常所说的标准正态分布均值为0, 标准差为1的正态分布。

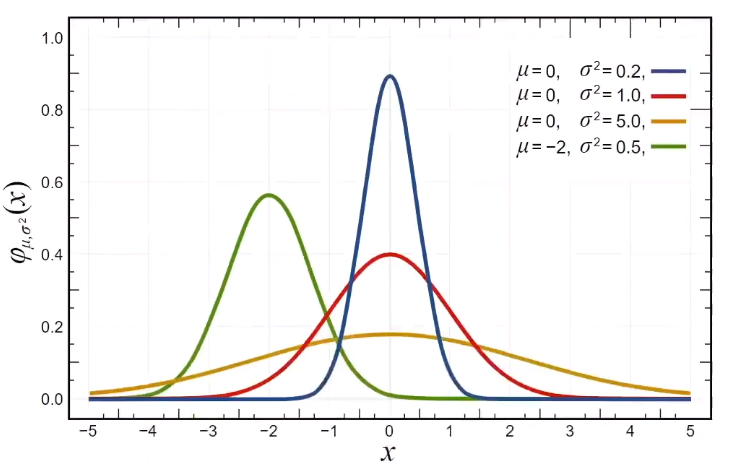
jupyter

3.4 随机变量的期望#

对于一个随机变量，时常要考虑它的平均取什么，期望就是概率中的平均值，对随机变量中心位置的一种度量。例子. 经过长期观察积累，某射手在每次射击中命中的坏数 $X$ 服从分布： $$ \begin{array}{|c|c|c|c|c|c|c|c|} \hline \mathrm{X} & 0 & 5 & 6 & 7 & 8 & 9 & 10 \\ \hline p_{i} & 0 & 0.05 & 0.05 & 0.1 & 0.1 & 0.2 & 0.5 \\ \hline \end{array} $$ 求这个射手平均命中的坏数是多少? 解一种很自然的考虑是：假定该射击手进行了100次射击，那么，约有5次命中5坏，5次命中6坏，10次命中7坏，10次命中8坏，20 次命中9坏，50次命10，没有脱革，从而在一次射击中，该射手平均命中的坏数为： $\frac{1}{100}(10 \times 50+9 \times 20+8 \times 10+7 \times 10+6 \times 5+5 \times 5+0 \times 0)=8.85$ 所以，我们可以看到离散型的随机变量的期望值可以表示为： $E(X)=\sum_{i=1}^{+\infty} x_{i} p_{k}$

期望的性质：

$E(c)=c$
$E(X+c)=E(X)+c$
$E(k X)=k E(X)$
$E(k X+c)=k E(X)+c$
$E(X+Y)=E(X)+E(Y)$

3.5 随机变量的方差：#

方差表示了随机变量的变异性，方差越大，随机变量的结果越不稳定。
定义：随机变量，若 $$ E[X-E(X)]^{2} $$ 存在，则称其为 $X$ 的方差，记为 $D(X),$ 即 $$ D(X)=E[X-E(X)]^{2} $$ 而称 $\sqrt{D(X)}$ 为 $X$ 的标准差或均方差。由方差的定义和数学期望的性质，可以推出方差的计算公式: $$ D(X)=E\left(X^{2}\right)-[E(X)]^{2} $$

方差的性质
(1) $D(c)=0$
(2) $D(X+c)=D(X)$
(3) $D(c X)=c^{2} D(X)$

例子：
甲、乙两车间生产同一种产品，设1000件产品中的次品数分别为随机变量 $X, Y,$ 已知他们的分布律如下:
$$ \begin{array}{ccccc} \mathbf{X} & \mathbf{0} & 1 & \mathbf{2} & \mathbf{3} \\ \hline p_{i} & 0.2 & 0.1 & 0.5 & 0.2 \end{array} $$ 与 $$ \begin{array}{|c|c|c|c|c|} \hline \mathrm{Y} & 0 & 1 & 2 & 3 \\ \hline p_{i} & 0.1 & 0.3 & 0.4 & 0.2 \\ \hline \end{array} $$ 试讨论甲乙两者车厢的质量。解先计算均值 $$ \begin{array}{l} E(X)=0 \times 0.2+1 \times 0.1+2 \times 0.5+3 \times 0.2=1.7 \\ E(Y)=0 \times 0.1+1 \times 0.3+2 \times 0.4+3 \times 0.2=1.7 \end{array} $$ 得到：甲、乙两车间次品数的均值相同。再计算方差： $D(X)=(0-1.7)^{2} \times 0.2+(1-1.7)^{2} \times 0.1+(2-1.7)^{2} \times 0.1+(2-1.7)^{2} \times 0.5+(3-1.7)^{2} \times 0.2=1.01$

$D(Y)=(0-1.7)^{2} \times 0.1+(1-1.7)^{2} \times 0.3+(2-1.7)^{2} \times 0.4+(2-1.7)^{2} \times 0.4+(3-1.7)^{2} \times 0.2=0.81$

得到 $D(X)>D(Y),$ 说明乙车间的产品质量较稳定。

随机模拟1：$\pi$的估值#

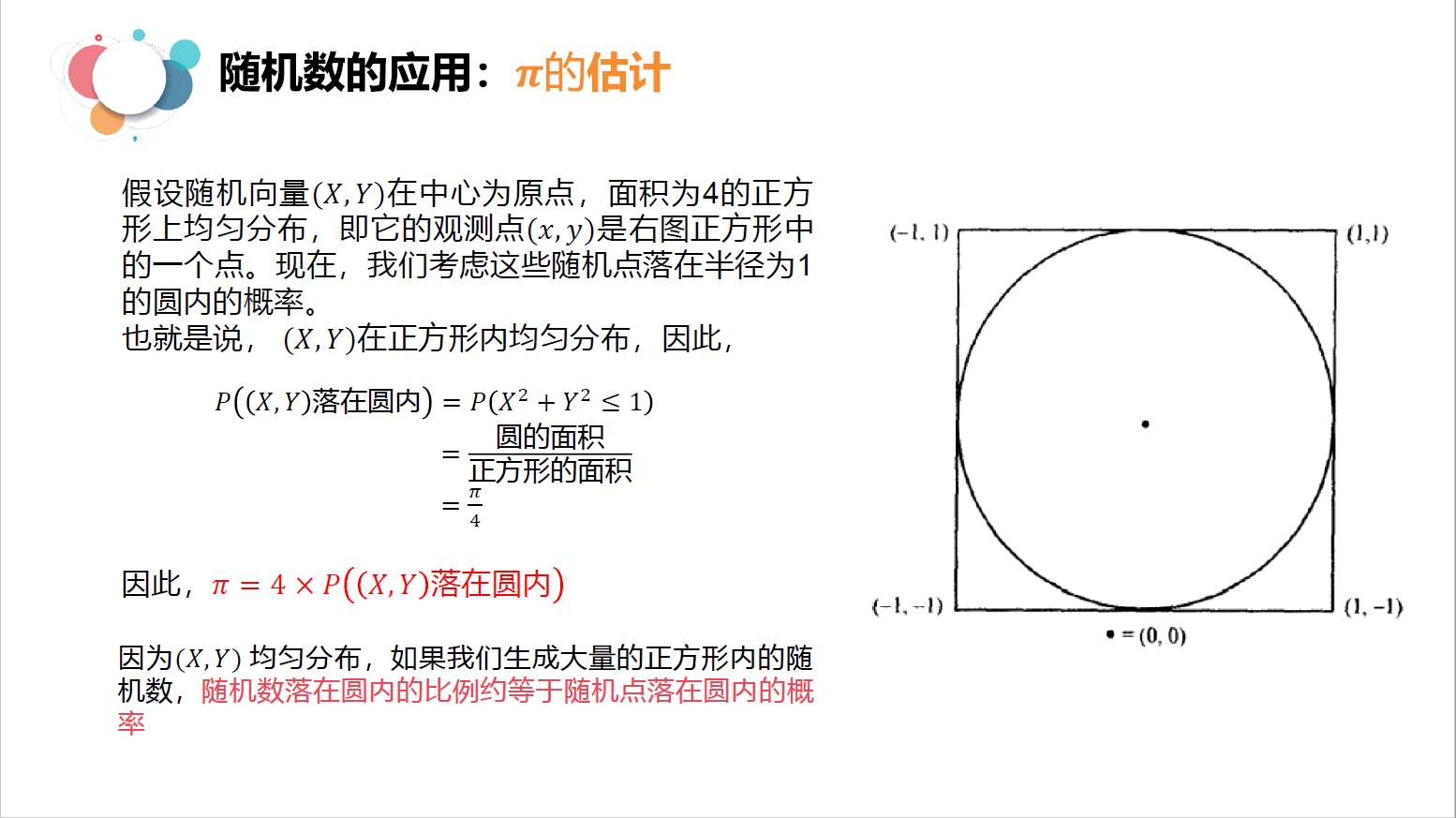
jupyter jupyter

# pi的估计问题
import numpy as np 
def pi_estimate(n):
    '''
    n为投点的数量
    '''
    n_rand_X = np.random.uniform(-1.0,1.0,n)
    n_rand_Y = np.random.uniform(-1.0,1.0,n)
    ## 判断是否在圆内
    distance = np.sqrt(n_rand_X**2 + n_rand_Y**2)
    dis_n = float(len(distance[distance<=1.0]))
    return 4 * (dis_n / n)

for i in [10,50,100,500,1000,5000,10000,50000,100000,500000,10000000]:
    print("pi的估计值为",pi_estimate(i))

pi的估计值为 2.8
pi的估计值为 2.8
pi的估计值为 3.08
pi的估计值为 3.112
pi的估计值为 3.132
pi的估计值为 3.1632
pi的估计值为 3.1516
pi的估计值为 3.1388
pi的估计值为 3.1388
pi的估计值为 3.138104

pi的估计值为 3.1416736

?np.random.uniform

随机模拟2:电子元件寿命问题#

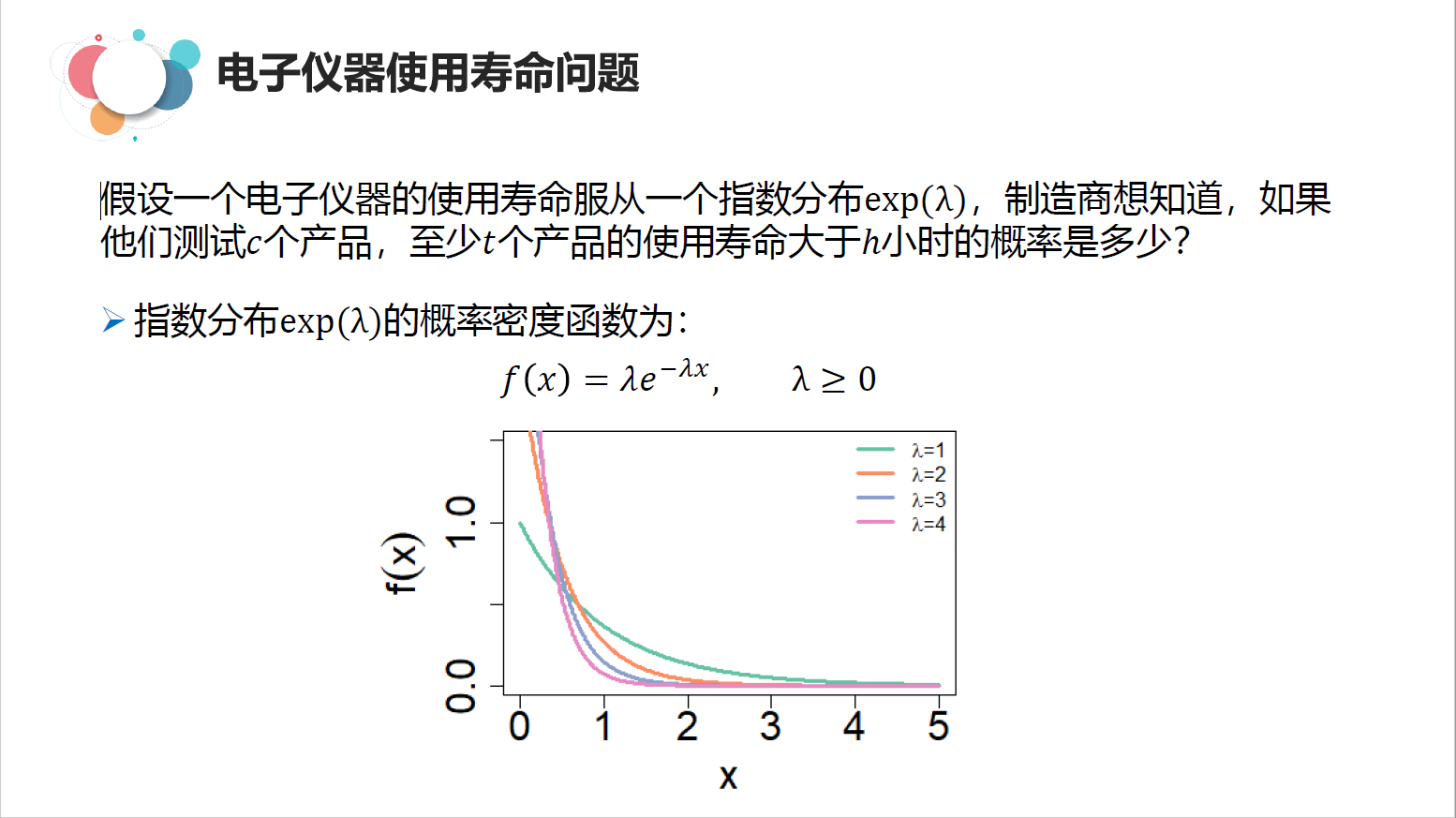
jupyter
jupyter

# 电子元件寿命问题
import numpy as np 

def ele_life(n,c,h,t,lamb):
    """
    参数n:模拟实验的次数
    参数c:每次试验中的c个元件
    参数t:每c个元件中规定的合格品数量
    参数h:小时数
    """
    times = 0.0
    for i in range(n):
        c_rand = np.random.exponential(1/lamb,c)
        c_rand_t = len(c_rand[c_rand>h])
        if c_rand_t > t:
            times = times + 1
    return times / n  

ele_life(10000,1000,18,20,0.2)

0.9133

?np.random.exponential

随机模拟3：三门问题#

蒙提霍尔问题：假如你参与一个有主持人的游戏，你会看见三扇关闭了的门，其中一扇的后面有一辆汽车，另外2扇门后面各是一只山羊，你看不见门后面的情况，但主持人知道一切。你被主持人要求在三扇门中选择一扇，但不能打开，在你选定之后主持人开启了另一扇后面有山羊的门，然后你可以坚持原来选定的门，也可以改主意重新选择。问题是：改与不改对选中汽车的概率有影响吗？请使用模拟实验的方法回答该问题。

# 三门问题
import numpy.random as random
def MontyHallProblem(n_test):
    #测试次数
     
    winning_door = random.randint(0,3,n_test)
    first_get  = 0
    change_get = 0
    for winning_doors in winning_door:
        act_door = random.randint(0,3)
        if winning_doors == act_door:
            first_get += 1
        else :
            change_get += 1
    first_pro  = first_get / n_test
    change_pro = change_get / n_test
    compar1    = round(change_get / first_get,2)
    print ("在%d次测试中,坚持原则第一次就选中的次数是%d,改变决定选择另一扇门中奖的次数是%d"% (n_test,first_get,change_get))
    print ("概率分别是{0}和{1}，改变决定选择另一扇门中奖几率是坚持选择的{2}倍".format(first_pro,change_pro,compar1))
MontyHallProblem(1000000)

在1000000次测试中,坚持原则第一次就选中的次数是333388,改变决定选择另一扇门中奖的次数是666612
概率分别是0.333388和0.666612，改变决定选择另一扇门中奖几率是坚持选择的2.0倍

CJKLab bioinfo

概率论与数理统计

Contents

概率论与数理统计#

1.随机事件与概率#

1.1 基础概念#

1.2 随机事件与概率#

1.3 条件概率#

1.4 事件的独立性#

2.全概率公式和贝叶斯公式#

2.1 全概率公式#

2.2 贝叶斯公式#

3.随机变量#

3.1 随机变量#

3.2 概率分布#

3.3 概率密度函数#

3.4 随机变量的期望#

3.5 随机变量的方差：#

随机模拟1：\(\pi\)的估值#

随机模拟2:电子元件寿命问题#

随机模拟3：三门问题#